Matemática
VIDEO 1 :Lógica e a argumentação na linguagem cotidiana
A linguagem cotidiana como fonte primeira do raciocínio lógico e linguagens matemáticas: relações. Proposições matemáticas: a dicotomia V ou F e a ausência de uma terceira possibilidade.As equações como modo de se fazer perguntas na linguagem matemática.As situações problema, os problemas e o equacionamento dos problemas com tradução das perguntas na linguagem matemática.
Prof Nilson Jose Machado
Matemática é uma linguagem
Matemática é apresentado como linguagem.Mas linguagem não é a língua alfabética ? A matemática tem
uma linguagem, um conjunto de técnicas, conteúdos, idéias fundamentais.
A matemática desenvolve o raciocinio lógico ? Sim, mas a fonte primário para o raciocínio lógico é a lingua materna.A matemática, a lógica e a língua materna estão entrelaçadas, combinado com proposições, argumentos e problemas.
Linguagem cotidiana
Na línguagem cotidiana, temos sentenças exclamativas, declarativas e interrogativas.A matemática é dependente da linguagem cotidiana.Ela é um conjunto de sentenças declarativas, ela somente declara verdadeiro ou falso, não há meio termo.Ela deixa de lado as exclamativas, as interrogativas.
Na matemática, as proposições, as frases, as sentenças são sempre V ou F.Não ha´como ser as duas coisas
ou uma terceira.Para conseguir isto, é preciso deixar as sentenças perigosas.Aristóteles, 300 a.C. filtrou as sentenças complicadas e trouxe pra lógica 4 proposições categóricas.
A matemática precisa se aproximar da lógica, no sentido mais amplo.Para aproximar é preciso enfrentar
ambiguidades nas sentenças declarativas e fazer perguntas.
A pergunta surge em uma situação de problema.Traduzir este problema em uma linguagem corrente e
traduzir em linguagem matemática, equacionando o problema e solucionando o mesmo.
Não há elementos para definir quem vai receber a menor parte.Se faltar um dado , o problema é defeituoso? Na vida temos a situação/problema.Ninguém sabe o que é necessário para recolver o problema posto. Descobrir o dado necessário para responder a pergunta, faz parte de resolver o problema.É importante ter consciência de que falta informações para a resolução do problema.
----------------------------------------------------------------------------------------------
Matemática
VIDEO 2 : Lógica e a argumentação na linguagem cotidiana
Proposições e Argumentos: distinção entre a verdade de uma proposição e a validade de um argumento. Estrutura básica do argumento em linguagem matemática: premissas e conclusão. Paradoxos, tautologias;
a ideia de demonstração. A forma de um argumento válido: exemplos da análise da validade de alguns argumentos. Distinção entre demonstrar e convencer.
Toda operação matemática tem uma argumentação de conclusão.Só sai da contradição com a apresentação
de boas argumentações.É lógico quando se apresenta demonstrações.
Prof Jose Luiz Pastore Mello
Médias
Arquitas de Tarento, 400 a.C., contemporâneo de Platão, definia:
Média aritmética é um número quando o excesso do primeiro para o segundo é igual ao excesso do segundo para o terceiro.Envolvia proporcionalidade tanto na aritmética quanto na geometria.É a média com respeito a operação de soma.
Geralmente ocorre no fornecimento de taxas de variação(velocidades, períodos, vazões,etc).
X-M = M-Y → Mh = 2XY
Proposições e Argumentos: distinção entre a verdade de uma proposição e a validade de um argumento. Estrutura básica do argumento em linguagem matemática: premissas e conclusão. Paradoxos, tautologias;
a ideia de demonstração. A forma de um argumento válido: exemplos da análise da validade de alguns argumentos. Distinção entre demonstrar e convencer.
Prof Nilson Jose Machado
Uma situação-problema gera perguntas sobre o contexto com uma linguagem que o problema surge para a linguagem matemática utilizando técnicas e recursos para a solução do problema.
A lógica trata de argumentos, argumentar é a questão central da lógica.Argumentar é defender uma proposição com apresentação de razões.Não é uma questão de natureza lógica eu achar que uma coisa é verdadeira.Uma sentença , ou é verdadeira, ou falsa.Uma argumentação, ou é válido ou não válido.Há coisas que realmente são verdadeiras e dispensa demontração.Teutologia é dizer que uma coisa é igual a si mesma.A é igual a A.Demonstrar o que não é tautológico sem chegar ás contradições.
A lógica não entra no conteúdo das proposições, só nas verdades ou falsidades.A lógica pode ser chamada
de Lógica Formal, que cuida da forma da argumentação.No ex 2 há muita ambiguidade, a argumentação é perfeita mas a verdade é duvidosa.A defesa da verdade de uma coisa depende de duas coisas independentes: de uma boa argumentação e da verdade das premissas.No ex 3, podem ser tudo verdade mas a argumentação é muito ruim, insustentável.
Toda operação matemática tem uma argumentação de conclusão.Só sai da contradição com a apresentação
de boas argumentações.É lógico quando se apresenta demonstrações.
Por que, ao analisar uma argumentação, ou começamos por premissas verdadeiras ou conclusão falsa? A resposta está neste vídeo.Aqui você também aprenderá a diferenciar um argumento válido de um argumento inválido.
-----------------------------------------------------------------------------------------------
Matemática
VIDEO 3 : Médias para todos os fins: significado, relações, propriedades
Definições das médias aritmética, geométrica e harmônica. Abordagens algébrica e geométrica da ordenação entre as três médias. Condição de igualdade entre as três médias. A média harmônica em um problema de cinemática.Prof Jose Luiz Pastore Mello
Médias
"As médias estão associadas á idéia de substituir uma sequência de números por um único que represente toda sequência.Elas, geralmente, estão associadas a uma determinada operação sobre a sequência dos números.
Média aritmética é um número quando o excesso do primeiro para o segundo é igual ao excesso do segundo para o terceiro.Envolvia proporcionalidade tanto na aritmética quanto na geometria.É a média com respeito a operação de soma.
Primeiro: X, segundo: M, Terceiro: Y, com X>M>Y
X-M=M-Y
Ma=X+Y
2
2
-----
Média Geométrica é um número quando a proporção do segundo para o terceiro é igual a do
primeiro para o segundo.É a média com respeito a operação de multiplicação.
M/Y=X/M → Mg = Vx.y
Aplicação:
- A altura de um triângulo retângulo em relação à hipotenusa é a média geomètrica das projeções ortogonais dos catetos sobre hipotenusa.
------
-Numa aplicação de juros composto, o fator de aumento médio é a média geométrica dos fatores
-Numa aplicação de juros composto, o fator de aumento médio é a média geométrica dos fatores
de aumentos individuais.
Média Harmônica é um número quando a quantidade que o primeiro excede o segundo em relação ao primeiro é igual a quantidade que o segundo excede o terceiro em relação ao terceiro.É a média com respeito a operação de soma dos inversos.
Geralmente ocorre no fornecimento de taxas de variação(velocidades, períodos, vazões,etc).
X-M = M-Y → Mh = 2XY
X Y X+Y
Apresentação Aritmética
A ordenação das médias é um assunto de grande interesse na matemática, pois por meio delas,
conseguimos resolver problemas complexos.Dado dois números (X Y), qual a média maior ? É
a aritmética, geométrica ou harmônica ? É sempre a mesma maior que a outra ?
a aritmética, geométrica ou harmônica ? É sempre a mesma maior que a outra ?
Apresentação Aritmética
Apresentação Geométrica
-----------------------------------------------------------------------------
Matemática
VIDEO 4 : Médias para todos os fins: significado, relações, propriedades
Definição da média quadrática. Dedução geométrica usando teorema de Pitágoras e semelhança de triângulos da ordenação entre as médias aritmética, geométrica, harmônica e quadrática. Desvios em relação à média. A média quadrática e a definição de desvio. A qualidade da média aritmética na minimização dos desvios. Definição de desvio padrão.
Prof Jose Luiz Pastore Mello
Media Quadrática é a raiz quadrada da média aritmética dos quadrados dos números.
Definição da média quadrática. Dedução geométrica usando teorema de Pitágoras e semelhança de triângulos da ordenação entre as médias aritmética, geométrica, harmônica e quadrática. Desvios em relação à média. A média quadrática e a definição de desvio. A qualidade da média aritmética na minimização dos desvios. Definição de desvio padrão.
Prof Jose Luiz Pastore Mello
Media Quadrática é a raiz quadrada da média aritmética dos quadrados dos números.
FÓRMULA DA MÉDIA QUADRÁTICA
A Média Quadrática é a maior ou igual de todas.Maior que a média aritmética, que a média geométrica e que a média harmônica.
----
----
Slides da Aula 4
----------------------------------------------------------------------------------------
Matemática
VIDEO 5 : ESTATÍSTICA PARA TODOS : NOÇÕES INICIAIS, CURVAS NORMAIS(1)
Análise dos principais tipos de amostragens. Cálculos e significados das medidas de tendência central e de dispersão, especialmente do desvio padrão. Apresentação da distribuição normal e da possibilidade de relacionarmos áreas sobre esta curva com probabilidades intervalares.
Análise dos principais tipos de amostragens. Cálculos e significados das medidas de tendência central e de dispersão, especialmente do desvio padrão. Apresentação da distribuição normal e da possibilidade de relacionarmos áreas sobre esta curva com probabilidades intervalares.
Prof Walter Spinelli
A estatística se preocupa em analisar as variáveis de diversas naturezas.Para isto, existe um método para sua realização.As pessoas organizam estes passos para sua execução: o que quer saber, um questionário e recolher estas variáveis para a formulação da estatística.Ela não é feita com a totalidade das pessoas e sim por uma parte.Esta parte á a mais difícil da seleção.
Estatística é a ciência que utiliza-se das teorias probabilísticas para explicar a frequência da ocorrência de eventos1 , tanto em estudos observacionais quanto em experimento modelar a aleatoriedade e a incerteza de forma a estimar ou possibilitar aprevisão de fenômenos futuros, conforme o caso.
Algumas práticas estatísticas incluem, por exemplo, o planejamento, a sumarização e a interpretação de observações. Dado que o objetivo da estatística é a produção da melhor informação possível a partir dos dados disponíveis, alguns autores sugerem que a estatística é um ramo da teoria da decisão.
Devido às suas raízes empíricas e seu foco em aplicações, a estatística geralmente é considerada uma disciplina distinta damatemática, e não um ramo dela.2 3
A estatística é uma ciência que se dedica à coleta, análise e interpretação de dados. Preocupa-se com os métodos de recolha, organização, resumo, apresentação e interpretação dos dados, assim como tirar conclusões sobre as características das fontes donde estes foram retirados, para melhor compreender as situações.
Tipos de amostras :
1 - Casual Simples
Faz-se um sorteio aleatório das pessoas que serão pesquisadas, de um modo simples.
2 - Sistemática
É aquela que precisa dividir a população em determinadas faixas, fazendo de maneira sistemática, pegando algumas pessoas de cada faixa.Ex: de 5 em cinco, de idade em idade, de cor em cor.
3 - Acidental
Trabalha dentro da população de modo objetivo, em um determinado foco, uma poulação alvo que te interessa.Ex:Pesquisa de satisfação de uma concessionária.Ex: o que a pessoa acha de um shampoo para cabelos castanhos, não vai pesquisa uma loira nem um careca.
4 - Estratificada
Trabalha com dados numéricos.Ex: pesquisa de consumo de eletricidade.A coleta de informação é diferente onde se consome mais com a que consome menos.
Para se ter uma amostragem mais fiel, precisa-se pesquisar pessoas de diversos níveis, tanto econômico, social, etário, etc.
Medidas de Tendência Central
Quando a média é tirada de valores extremos, ela tem pouco significado.O certo é associar á outras medidas.
A moda e a mediana são, assim como a média, medidas de tendência central de um conjunto de dados. São chamadas também de medidas de posição, pois servem para "resumir", em apenas uma informação, a característica desse conjunto de dados.
Dependendo da situação, é mais conveniente usar a média, a moda ou a mediana.
A partir das medidas das alturas de um grupo de pessoas, é possível calcular uma altura que caracteriza o grupo todo.
Conhecendo as notas de um aluno durante um semestre da faculdade, é possível calcular uma nota que "resume" a sua situação no semestre.
Com base no número de gols de um time, em várias partidas de um campeonato, é possível chegar a um número de gols que descreva a sua situação no campeonato.
Observando os tempos de viagem de um determinado ônibus, em várias viagens, é possível se chegar a um valor que indica, em geral, o tempo dessa viagem.
Média Aritmética
Multiplica a média das notas com a frequência e divide por 100 elementos = 5,7
É um número quando o excesso do primeiro para o segundo é igual ao excesso do segundo para o terceiro.Envolvia proporcionalidade tanto na aritmética quanto na geometria.É a média com respeito a operação de soma.
Mediana
Medida central ordenando os termos = 5,1
Mediana é uma medida de tendência central que indica exatamente o valor central de uma amostra de dados.
Exemplos:
As notas de um aluno em um semestre da faculdade, colocadas em ordem crescente, foram: 4,0; 4,0; 5,0; 7,0; 7,0. São cinco notas. A mediana é o valor que está no centro da amostra, ou seja, 5,0. Podemos afirmar que 40% das notas estão acima de 5,0 e 40% estão abaixo de 5,0.
A quantidade de hotéis 3 estrelas espalhados pelas cidades do litoral de um determinado Estado é: 1, 2, 3, 3, 5, 7, 8, 10, 10, 10. Como a amostra possui dez valores e, portanto, não há um valor central, calculamos a mediana tirando a média dos dois valores centrais:
Assim, há exatamente 50% das cidades com mais de 6 hotéis três estrelas e 50% das cidades com menos de 6 hotéis três estrelas.
Dessa forma, podemos resumir o cálculo da mediana da seguinte forma:
- os valores da amostra devem ser colocados em ordem crescente ou decrescente;
- se a quantidade de valores da amostra for ímpar, a mediana é o valor central da amostra. Nesse caso, há a mesma quantidade de valores acima e abaixo desse valor;
- se a quantidade de valores da amostra for par, é preciso tirar a média dos valores centrais para calcular a mediana. Nesse caso, 50% dos valores da amostra estão abaixo e 50% dos valores da amostra estão acima desse valor.
Moda
Moda é o valor mais frequente, o maior valor = O valor correto é 6,5
Moda é a medida de tendência central que consiste no valor observado com mais frequência em um conjunto de dados.
Se um determinado time fez, em dez partidas, a seguinte quantidade de gols: 3, 2, 0, 3, 0, 4, 3, 2, 1, 3, 1; a moda desse conjunto é de 3 gols.
Se uma linha de ônibus registra, em quinze ocasiões, os tempos de viagens, em minutos: 52, 50, 55, 53, 61, 52, 52, 59, 55, 54, 53, 52, 50, 51, 60; a moda desse conjunto é de 52 minutos.
As alturas de um grupo de pessoas são: 1,82 m; 1,75 m; 1,65 m; 1,58 m; 1,70 m. Nesse caso, não há moda, porque nenhum valor se repete.
Medidas de Dispersão
Amplitude
É a faixa de variação dos dados numéricos, do maior para o menor.Ex: A amplitude entre 10 e 1 é 9.
A amplitude é definida como sendo a diferença entre o maior e o menor valor do conjunto de dados. Denotaremos a amplitude por R.Como o valor máximo do conjunto é 72 e o valor mínimo é 60, temos que a amplitude é:
é a comparação da média com os elementos, soma estas diferenças e divide pelo total de elementos.
É a média diferenças da média.
Desvio Padrão
É o desvio médio elevado ao quadrado tirando sua raiz quadrada, não importando se é negativa ou positiva.Uma vez que a variância envolve a soma de quadrados, a unidade em que se exprime não é a mesma que a dos dados. Assim, para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados, tomamos a raiz quadrada da variância e obtemos o desvio padrão:
O desvio padrão é uma medida que só pode assumir valores não negativos e quanto maior for, maior será a dispersão dos dados.
4 - Estratificada
Trabalha com dados numéricos.Ex: pesquisa de consumo de eletricidade.A coleta de informação é diferente onde se consome mais com a que consome menos.
Para se ter uma amostragem mais fiel, precisa-se pesquisar pessoas de diversos níveis, tanto econômico, social, etário, etc.
Medidas de Tendência Central
Quando a média é tirada de valores extremos, ela tem pouco significado.O certo é associar á outras medidas.
A moda e a mediana são, assim como a média, medidas de tendência central de um conjunto de dados. São chamadas também de medidas de posição, pois servem para "resumir", em apenas uma informação, a característica desse conjunto de dados.
Dependendo da situação, é mais conveniente usar a média, a moda ou a mediana.
A partir das medidas das alturas de um grupo de pessoas, é possível calcular uma altura que caracteriza o grupo todo.
Conhecendo as notas de um aluno durante um semestre da faculdade, é possível calcular uma nota que "resume" a sua situação no semestre.
Com base no número de gols de um time, em várias partidas de um campeonato, é possível chegar a um número de gols que descreva a sua situação no campeonato.
Observando os tempos de viagem de um determinado ônibus, em várias viagens, é possível se chegar a um valor que indica, em geral, o tempo dessa viagem.
Média Aritmética
Multiplica a média das notas com a frequência e divide por 100 elementos = 5,7
É um número quando o excesso do primeiro para o segundo é igual ao excesso do segundo para o terceiro.Envolvia proporcionalidade tanto na aritmética quanto na geometria.É a média com respeito a operação de soma.
Mediana
Medida central ordenando os termos = 5,1
Mediana é uma medida de tendência central que indica exatamente o valor central de uma amostra de dados.
Exemplos:
As notas de um aluno em um semestre da faculdade, colocadas em ordem crescente, foram: 4,0; 4,0; 5,0; 7,0; 7,0. São cinco notas. A mediana é o valor que está no centro da amostra, ou seja, 5,0. Podemos afirmar que 40% das notas estão acima de 5,0 e 40% estão abaixo de 5,0.
A quantidade de hotéis 3 estrelas espalhados pelas cidades do litoral de um determinado Estado é: 1, 2, 3, 3, 5, 7, 8, 10, 10, 10. Como a amostra possui dez valores e, portanto, não há um valor central, calculamos a mediana tirando a média dos dois valores centrais:
Assim, há exatamente 50% das cidades com mais de 6 hotéis três estrelas e 50% das cidades com menos de 6 hotéis três estrelas.
Dessa forma, podemos resumir o cálculo da mediana da seguinte forma:
- os valores da amostra devem ser colocados em ordem crescente ou decrescente;
- se a quantidade de valores da amostra for ímpar, a mediana é o valor central da amostra. Nesse caso, há a mesma quantidade de valores acima e abaixo desse valor;
- se a quantidade de valores da amostra for par, é preciso tirar a média dos valores centrais para calcular a mediana. Nesse caso, 50% dos valores da amostra estão abaixo e 50% dos valores da amostra estão acima desse valor.
Moda
Moda é o valor mais frequente, o maior valor = O valor correto é 6,5
Moda é a medida de tendência central que consiste no valor observado com mais frequência em um conjunto de dados.
Se um determinado time fez, em dez partidas, a seguinte quantidade de gols: 3, 2, 0, 3, 0, 4, 3, 2, 1, 3, 1; a moda desse conjunto é de 3 gols.
Se uma linha de ônibus registra, em quinze ocasiões, os tempos de viagens, em minutos: 52, 50, 55, 53, 61, 52, 52, 59, 55, 54, 53, 52, 50, 51, 60; a moda desse conjunto é de 52 minutos.
As alturas de um grupo de pessoas são: 1,82 m; 1,75 m; 1,65 m; 1,58 m; 1,70 m. Nesse caso, não há moda, porque nenhum valor se repete.
Medidas de Dispersão
Amplitude
É a faixa de variação dos dados numéricos, do maior para o menor.Ex: A amplitude entre 10 e 1 é 9.
A amplitude é definida como sendo a diferença entre o maior e o menor valor do conjunto de dados. Denotaremos a amplitude por R.Como o valor máximo do conjunto é 72 e o valor mínimo é 60, temos que a amplitude é:
R = 72 - 60 = 12.
Desvio Médioé a comparação da média com os elementos, soma estas diferenças e divide pelo total de elementos.
É a média diferenças da média.
Desvio Padrão
É o desvio médio elevado ao quadrado tirando sua raiz quadrada, não importando se é negativa ou positiva.Uma vez que a variância envolve a soma de quadrados, a unidade em que se exprime não é a mesma que a dos dados. Assim, para obter uma medida da variabilidade ou dispersão com as mesmas unidades que os dados, tomamos a raiz quadrada da variância e obtemos o desvio padrão:
O desvio padrão é uma medida que só pode assumir valores não negativos e quanto maior for, maior será a dispersão dos dados.
Algumas propriedades do desvio padrão, que resultam imediatamente da definição, são:
o desvio padrão será maior, quanta mais variabilidade houver entre os dados.

Medidas de Dispersão: variância, desvio padrão e coeficiente de variação
Videoaula elaborada pelo professor Rodrigo Itaboray Fra
SLIDES AULA 5
VIDEO 6 : ESTATÍSTICA PARA TODOS : NOÇÕES INICIAIS, CURVAS NORMAIS(2)
 (1+2+3+4+...+n)
(1+2+3+4+...+n)
o desvio padrão será maior, quanta mais variabilidade houver entre os dados.
Medidas de Dispersão: variância, desvio padrão e coeficiente de variação
Videoaula elaborada pelo professor Rodrigo Itaboray Fra
SLIDES AULA 5
------------------------------------------------------------------------------
VIDEO 6 : ESTATÍSTICA PARA TODOS : NOÇÕES INICIAIS, CURVAS NORMAIS(2)
Apresentação do cálculo do desvio padrão das proporções. Interpretação de situações nas quais as probabilidades de ocorrências de eventos em certas faixas, em certos intervalos, podem ser associadas à áreas sob a curva normal. Discussão sobre a fixação de intervalos de confiança para resultados esperados em pesquisas, e análise da situação específica de uma pesquisa eleitoral.
Prof Walter Spinelli




Para definirmos desvio padrão é necessário definir variância. A notação mais comumente usada é:
- s2: variância amostral.
- σ2: variância populacional.
- s : desvio padrão amostral.
- σ : desvio padrão populacional.
Variância populacional
A variância de uma população {x1,...,xN} de N elementos é a medida de dispersão definida como a média do quadrado do desvios dos elementos em relação à média populacional μ. Ou seja, a variância populacional é dada por:
Variância amostral
A variância de uma amostra {x1,...,xn} de n elementos é definida como a soma dos quadrados dos desvios de elementos em relação à sua média  dividido por (n-1). Ou seja, a variância amostral é dada por:
dividido por (n-1). Ou seja, a variância amostral é dada por:
Ao utilizarmos a média amostral como estimador de m para calcularmos a variância amostral, perdemos 1 grau de liberdade em relação à variância populacional.
Desvio padrão populacional
O desvio padrão populacional de um conjunto de dados é igual à raiz quadrada da variância populacional. Desta forma, o desvio padrão populacional é dado por:
Desvio padrão amostral
O desvio padrão amostral de um conjunto de dados é igual à raiz quadrada da variância amostral. Desta forma, o desvio padrão amostral é dado por:
-----------------------------------------------------------------------------------------------------
Matemática
VIDEO 7 : SEQUÊNCIAS, REGULARIDADES E SÉRIES
Identificação e representação de sequências. Fórmulas recursivas (recorrência) e posicionais. Contextos de aplicação das sequências aritméticas e geométricas: movimento uniforme e matemática financeira. Números figurados. Sequência de Fibonacci.
Prof Jose Luiz Pastore Mello
Uma sucessão ou sequência é uma listagem de termos ou elementos que, no sentido usual, são indexados por um conjunto contável em ordem a permitir identificar um termo inicial. Defini-se o tamanho de uma sequência pelo número de elementos que esta possuí, podendo existir sequências ou infinitas ou finitas.
Definição informal
Informalmente, uma sequência é um conjunto  dotado das seguintes características:
dotado das seguintes características:
- Os elementos também são denominados termos da sucessão;
- Cada termo possui uma posição definida, dentro do conjunto
- A posição de cada termo é determinada por um número natural, denominado índice;
- Cada termo possui um único índice, e cada índice pertence a um único termo (correspondência biunívoca);
- Dois termos só podem ser permutados se os seus respectivos índices também forem.
Definição formal
Em análise matemática, define-se uma sequência como uma função  definida sobre um subconjunto
definida sobre um subconjunto  dos números naturais que toma elementos no conjunto
dos números naturais que toma elementos no conjunto  .2
.2
Sequências
Sequência de números reais
Sequências infinitas
Uma sequência numérica infinita é uma função  , tal que
, tal que  . Representa-se uma sequência infinita, em geral, escrevendo seus termos iniciais seguidos de reticências, por exemplo,
. Representa-se uma sequência infinita, em geral, escrevendo seus termos iniciais seguidos de reticências, por exemplo,  , ou apresentando seu termo geral quando conhecido,
, ou apresentando seu termo geral quando conhecido,  . Meramente queremos indicar que todo termo possuí um sucessor.
. Meramente queremos indicar que todo termo possuí um sucessor.
Sequências monótonas
Diz-se que uma sequência  é crescente se
é crescente se  ; e decrescente se
; e decrescente se 
Diz-se que a sequência é não-decrescente se  , e não-crescente se
, e não-crescente se 
Uma sequência é monótona se satisfaz qualquer uma das condições descritas acima.
Progressão aritmética
Origem: Wikipédia, a enciclopédia livre.
Uma progressão aritmética (abreviadamente, P. A.) é uma sequência numérica em que cada termo, a partir do segundo, é igual à soma do termo anterior com uma constante  O número
O número  é chamado de razão ou diferença comum da progressão aritmética.1
é chamado de razão ou diferença comum da progressão aritmética.1
Alguns exemplos de progressões aritméticas:
- 1, 4, 7, 10, 13, ..., é uma progressão aritmética em que a razão (a diferença entre os números consecutivos) é igual a 3.
- -2, -4, -6, -8, -10, ..., é uma P.A. em que
- 6, 6, 6, 6, 6, ..., é uma P.A. com
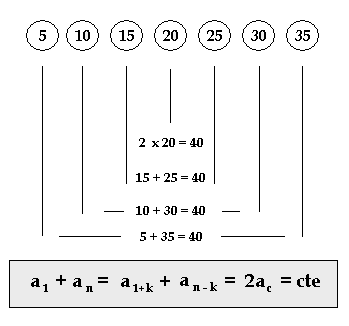
Numa progressão aritmética, a partir do segundo termo, o termo central é a média aritmética do termo antecessor e do sucessor, isto é, 
Fórmula do termo geral de uma progressão aritmética
O n-ésimo termo de uma progressão aritmética, denotado por  pode ser obtido por meio da formula1
pode ser obtido por meio da formula1
em que:
é o primeiro termo;
é a razão.
Por meio da formula acima também é possível inserir (ou interpolar) uma quantidade de meios aritméticos entre dois números dados, de modo que eles formem parte de uma progressão aritmética. Esse procedimento é chamado de interpolação aritmética.[carece de fontes]
Demonstração
A fórmula do termo geral pode ser demonstrada por indução matemática:
- Ela é válida para o segundo termo pois, por definição, cada termo é igual ao anterior mais uma constante fixa r e portanto
- Assumindo como hipótese de indução que a fórmula é válida para
ou seja, que
resulta que o n-ésimo termo é dado por:
De forma análoga, demonstra-se a seguinte fórmula, que expressa o n-ésimo termo em função do m-ésimo termo, para quaisquer inteiros positivos m e n:
Soma dos termos de uma progressão aritmética
A soma dos termos de uma progressão aritmética situados no intervalo fechado de  até
até  é calculada pela seguinte fórmula:
é calculada pela seguinte fórmula:
Em particular, para somar os n primeiros termos, pode-se utilizar a seguinte simplificação da fórmula anterior:
Demonstrações:
Considerando a PA  a soma
a soma  de todos os termos dessa progressão pode ser escrita assim:
de todos os termos dessa progressão pode ser escrita assim:
Somando membro a membro, obtemos:
Todos os pares entre parênteses têm o mesmo valor por serem simétricos em relação aos extremos da PA
e assim por diante
Então, como há  pares de termos:
pares de termos:
Tipos de progressões aritméticas
Progressão aritmética constante[
Uma progressão aritmética constante ou estacionária é toda progressão aritmética em que todos os termos são iguais, sendo que para isso a razão r tem que ser sempre igual a zero.
Exemplos de progressões aritméticas constantes:
- 5, 5, 5, 5, 5, ..., tem razão r = 0
- 0, 0, 0, 0, 0, ..., tem razão r = 0
Progressão aritmética crescente
Uma progressão aritmética crescente é toda progressão aritmética em que cada termo, a partir do segundo, é maior que o termo que o antecede, sendo que para isso a razão r tem que ser sempre maior que zero (r>0).
Exemplos de progressões aritméticas crescentes:
- 2, 4, 6, 8, 10, ..., com razão r = 2
- 3, 6, 9, 12, 15, ..., com razão r = 3
Progressão aritmética decrescente
Uma progressão aritmética decrescente é toda progressão aritmética em que cada termo, a partir do segundo, é menor que o termo que o antecede, sendo que para isso a razão r tem que ser sempre menor do que zero (r<0 p="">
Exemplos de progressões aritméticas decrescentes:
- 6, 4, 2, 0, -2, ..., tem razão igual a -2
- 6, 3, 0, -3, -6, ..., tem razão igual a -3
Progressão aritmética de segunda ordem
Uma progressão aritmética de segunda ordem é uma sequência de números em que as diferenças entre os termos consecutivos segue uma progressão aritmética. Por exemplo, na sequência
- 1, 3, 7, 13, 21, 31, 43, 57, 73, ...,
se subtrairmos o primeiro termo da sequência do segundo, teremos como resultado o número 2. Já a diferença entre o segundo e terceiro termos é igual a 4, a diferença entre o terceiro e o quarto termos é igual a 6, e assim sucessivamente. Verificamos que a diferença entre os termos da sequência cresce em progressão aritmética de razão igual a 2, ou seja, assume os valores 2, 4, 6, 8 e assim por diante.
Seguindo o mesmo raciocínio, podemos definir progressões aritméticas de ordem 3: são sequências numéricas cuja diferença entre os termos formam uma progressão aritmética de ordem 2. Por analogia, podemos definir progressões aritméticas de ordem n.2
O estudo da soma dos termos dessas sequências serve como introdução ao cálculo de integrais de funções polinomiais.[
A Progressão Geométrica é uma sucessão recursiva  definida assim:
definida assim:
(definição da função g)
(fórmula do termo geral)
(fórmula da recursão geométrica, que é outra maneira de se calcular  )
)
e q são constantes previamente definidas
Exemplos de P.G.:
- (
= 1, q = 1):
- (
= 3, q = -1):
Número triangular
Origem: Wikipédia, a enciclopédia livre.
Um número triangular é um número natural que pode ser representado na forma de triângulo equilátero. Foi desenvolvido por Gauss em 1788 quando ele tinha somente 10 anos. Para encontrar o n-ésimo número triangular a partir do anterior basta somar-lhe n unidades. Os primeiros números triangulares (sequência A000217 na OEIS) são:
Em geral, o n-ésimo número triangular é dado por:
Explicação Simplificada
Número Triangular Natural vezes o mesmo número, mais 1, dividido por dois igual a resultado do número Triangular.
Tal conceito é utilizado de maneira mais generalizada em progressões aritméticas.
Propriedades
Tem-se:
- Todo número perfeito par é triangular
- Os números triangulares de ordem ímpar são números hexagonais
Leonardo Fibonacci
Origem: Wikipédia, a enciclopédia livre.
| Leonardo Fibonacci | |
|---|---|
| Matemática | |
| Dados gerais | |
| Nome de nascimento | Leonardo Fibonacci |
| Nacionalidade | |
| Nascimento | c. 1170 |
| Local | Pisa |
| Morte | c. 1250 |
| Local | Pisa (?) |
Leonardo Fibonacci, também conhecido como Leonardo de Pisa, Leonardo Pisano ou ainda Leonardo Bigollo, (Pisa, c. 1170 — Pisa ?, c. 1250)1 mas, na maioria das vezes, simplesmente como Fibonacci foi um matemático italiano, tido como o primeiro grande matemático europeu da Idade Média. É considerado por alguns como o mais talentoso matemático ocidental da Idade Média.2 Ficou conhecido pela descoberta da sequência de Fibonacci e pelo seu papel na introdução dos algarismos arábicos na Europa.
Com outros matemáticos do seu tempo, contribuiu para o renascimento das ciências exatas, após a decadência do último período daantiguidade clássica e do início da Idade Média, mas Fibonacci destacou-se ao escrever o Liber Abaci, em 1202 (atualizado em 1254), a primeira obra importante sobre matemática desde Eratóstenes, isto é, mais de mil anos antes. O Liber Abaci introduziu os numerais hindu-arábicos na Europa, além de discutir muitos problemas matemáticos.3
Fibonacci é também conhecido pela sequência numérica nomeada após sua morte como sequência de Fibonacci. Ele não descobriu, mas usou-a como exemplo no Liber Abaci.4
A Sequência de Fibonacci
A Sequência de Fibonacci consiste em uma sucessão de números, tais que, definindo os dois primeiros números da sequência como 0 e 1, os números seguintes serão obtidos por meio da soma dos seus dois antecessores. Portanto, os números são: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181...
Dessa sequência, ao se dividir qualquer número pelo anterior, extrai-se a razão que é uma constante transcendental conhecido como número de ouro.
A sequência de Fibonacci é dada pela fórmula:
Uma das aplicações da sequência de Fibonacci é a identidade de Cassini.
Resolver uma relação de recorrência é encontrar uma fórmula explícita que dá o termo geral da sequência, de preferência usando funções elementares ou outras relações de recorrência mais simples.
Exemplo
Seja a sequência  , definida por:
, definida por:
- 1- Condição Básica:
;
- 2- Relação de Recorrência:
–
, para
.
Através desta sequência observamos que:
- -
- -
- -
- Por meio dos resultados podemos conjecturar que
, o que nos dá uma equação para o cálculo direto de
sem utilizarmos recorrência. Esta equação é denominada de Solução em Forma Fechada para a relação de recorrência, sujeita à condição básica
.
------------------------------------------------------------------------------------------------------
Matemática
VIDEO 8 : SEQUÊNCIAS, REGULARIDADES E SÉRIES (2)
Sequência aritmética de primeira e de segunda ordem. Sequências de números primos, de Grandi, harmônica, das aproximações de 2 ao quadrado e geométrica. Uma primeira definição de séries convergentes e divergentes. A convergência das séries geométricas de razão entre -1 e 1. A divergência da série harmônica.
Série (matemática)
Esta generalização, longe de acontecer de forma impune, traz diversas dificuldades:
- nem sempre é possível definir um valor resultante da soma para uma série;
- não é possível em geral trocar a ordem dos termos da série;
- algumas séries possuem soma infinita.
Embora a ideia de soma infinita seja bastante antiga, uma formulação matemática rigorosa só veio a surgir no século XVIII, com o advento da análise real, que denota e define uma série de termos  da seguinte forma:
da seguinte forma:
A teoria das séries divergentes generaliza este conceito de soma para alguns casos quando este limite não existe.
Um primeiro exemplo
Considere a dízima periódica que resulta da divisão de 1 por 3:
Esta dízima pode ser reinterpretada como a soma da série:
E neste caso, dizemos que a soma desta série é 
Notação
Se forem  os termos da sequência que desejamos somar. A soma
os termos da sequência que desejamos somar. A soma  da série será:
da série será:
No exemplo anterior, temos  , que forma uma progressão geométrica de razão
, que forma uma progressão geométrica de razão  .
.
Chamamos de soma parcial até o termo N,  a soma dos N primeiros termos de uma série:
a soma dos N primeiros termos de uma série:
Definição
Define-se a soma  de uma série infinita, o limite das somas parciais quando este limite existe:
de uma série infinita, o limite das somas parciais quando este limite existe:
Quando este limite existe, definímos ainda o resíduo de ordem n da série, pela seguinte série:
Esta definição nos permite escrever:
para todo
A soma parcial pode, portanto, ser interpretada como uma aproximação para a soma da série, enquanto que o resíduo é o erro desta aproximação.
Tipos importantes de séries
Série geométrica
A série geométrica formada pelos termos de uma progressão geométrica:Da teoria das progressões geométricas, temos que:É facil ver que seentão esta série é convergente e sua soma é dada por:
ou, como é mais usual:Série harmônica
A série harmônica formada pelos termos de uma progressão harmônica:Esta série é divergente, o que pode ser provado com a seguinte astúcia:e substitua nas somas parciais:Simplificando os termos repetidos temos:Série Infinita
Origem: Wikipédia, a enciclopédia livre.Em matemática a expressão, 1 − 2 + 3 − 4 + … é uma série infinita cujos termos são números inteiros, que vão alternando seus sinais. Utilizando a notação matemática para adição, a soma dos m primeiros termos da série se expressa como:Contudo, em meados do século XVIII, Leonhard Euler descobriu a seguinte relação qualificando-a de paradoxal:Foi somente muito tempo depois que se chegou a uma explicação rigorosa desta relação. Até o começo da década de 1890, Ernesto Cesàro e Émile Borel, entre outros, pesquisaram métodos bem definidos para atribuir somas generalizadas às séries divergentes — incluindo novas interpretações dos intentos realizados por Euler. Muitos destes métodos denominados da soma atribuem a (1 − 2 + 3 − 4 + …) uma "soma" de ¹⁄4. O método da soma de Cesàro é um dos poucos métodos que não soma a série 1 − 2 + 3 − 4 + …, por isso, esta série é um exemplo de um caso onde deve utilizar-se um método mais robusto como, por exemplo, o método da soma de Abel.A série 1 − 2 + 3 − 4 + … encontra-se relacionada com a série de Grandi 1 − 1 + 1 − 1 + …. Euler analisou estas duas séries como casos especiais de (1 − 2n + 3n − 4n + …) para valores de n aleatórios, uma linha de investigação que estende sua contribuição ao problema da Basiléia e conduz às equações funcionais do que conhecemos hoje como afunção eta de Dirichlet e a função zeta de Riemann.Série divergente
Origem: Wikipédia, a enciclopédia livre.Em matemática, uma série divergente é uma série que não converge. Tais séries são somas infinitas de parcelas que obedecem a uma regra e/ou Termo Geral. Se uma série converge, os termos individuais da série devem tender a zero. Portanto, toda série na qual os termos individuais não tendem a zero, diverge. O exemplo mais simples de uma série divergente cujos termos aproximam-se de zero é a série harmônicaA divergência da série harmônica foi demonstrada de forma distinta pelo matemático medieval Nicole d'Oresme.Às vezes é possível atribuir um valor às séries divergentes utilizando o método da soma. Por exemplo, a soma de Cesàro atribui à série divergente de Grandio valor ½. Em física, existe uma ampla variedade de métodos da soma.Série convergente
Origem: Wikipédia, a enciclopédia livre.Em matemática, uma série é o somatório dos termos de uma sequência de números.Dada uma sequência, a n-ésima soma parcial
é a soma dos primeiros n termos da sequência, isto é,
Uma série é convergente se a sequência de suas somas parciaisconverge. Em uma linguagem mais formal, uma série converge se existe um limite
tal que para qualquer número positivo arbitrariamente pequeno
, existe um inteiro
tal que para todo
,
Uma série que não é convergente é dita ser divergente.-
- ----------------------------------------------------------------------------------------------------------
- Probabilidade teórica: uma reconstituição histórica das diversas interpretações conhecidas sobre os cálculos probabilísticos, com apresentação de alguns problemas típicos.
- Prof Walter Spinelli
- PROBABILIDADE
- aleatoriedade x determinismo
Probabilidade
Origem: Wikipédia, a enciclopédia livre.Tal como acontece com a teoria da mecânica, que atribui definições precisas a termos de uso diário, como trabalho e força, também ateoria das probabilidades tenta quantificar a noção de provável.Em essência, existe um conjunto de regras matemáticas para manipular a probabilidade, listado no tópico "Formalização da probabilidade" abaixo. (Existem outras regras para quantificar a incerteza, como a teoria de Dempster-Shafer e a lógica difusa (em inglês fuzzy logic), mas estas são, em essência, diferentes e incompatíveis com as leis da probabilidade tal como são geralmente entendidas). No entanto, está em curso um debate sobre o que é, exatamente, que as regras se aplicam; a este tópico chama-se interpretações da probabilidade.Conceitos de probabilidade
A ideia geral da probabilidade é frequentemente dividida em dois conceitos relacionados:- Probabilidade de frequência ou probabilidade aleatória, que representa uma série de eventos futuros cuja ocorrência é definida por alguns fenômenos físicos aleatórios. Este conceito pode ser dividido em fenômenos físicos que são previsíveis através de informação suficiente e fenômenos que são essencialmente imprevisíveis. Um exemplo para o primeiro tipo é uma roleta, e um exemplo para o segundo tipo é um decaimento radioativo.
- Probabilidade epistemológica ou probabilidade Bayesiana, que representa nossas incertezas sobre proposições quando não se tem conhecimento completo das circunstâncias causativas. Tais proposições podem ser sobre eventos passados ou futuros, mas não precisam ser. Alguns exemplos de probabilidade epistemológica são designar uma probabilidade à proposição de que uma lei da Física proposta seja verdadeira, e determinar o quão "provável" é que um suspeito cometeu um crime, baseado nas provas apresentadas.
É uma questão aberta se a probabilidade aleatória é redutível à probabilidade epistemológica baseado na nossa inabilidade de predizer com precisão cada força que poderia afetar o rolar de um dado, ou se tais incertezas existem na natureza da própria realidade, particularmente em fenômenos quânticos governados pelo princípio da incerteza de Heisenberg. Embora as mesmas regras matemáticas se apliquem não importando qual interpretação seja escolhida, a escolha tem grandes implicações pelo modo em que a probabilidade é usada para modelar o mundo real.Representação e interpretação de valores de probabilidade
A probabilidade de um evento geralmente é representada como um número real entre 0 e 1. um evento impossível tem uma probabilidade de exatamente 0, e um evento certo de acontecer tem uma probabilidade de 1, mas a recíproca não é sempre verdadeira: eventos de probabilidade 0 não são sempre impossíveis, nem os de probabilidade 1 certos. A distinção bastante sutil entre "evento certo" e "probabilidade 1" é tratado em maior detalhe no artigo sobre "quase-verdade".A maior parte das probabilidades que ocorrem na prática são números entre 0 e 1, que indica a posição do evento no contínuo entre impossibilidade e certeza. Quanto mais próxima de 1 seja a probabilidade de um evento, mais provável é que o evento ocorra. Por exemplo, se dois eventos forem ditos igualmente prováveis, como por exemplo em um jogo de cara ou coroa, podemos exprimir a probabilidade de cada evento - cara ou coroa - como "1 em 2", ou, de forma equivalente, "50%", ou ainda "1/2".Probabilidades também podem ser expressas como chances (odds). Chance é a razão entre a probabilidade de um evento e à probabilidade de todos os demais eventos. A chance de obtermos cara, ao lançarmos uma moeda, é dada por (1/2)/(1 - 1/2), que é igual a 1/1. Isto é expresso como uma "chance de 1 para 1" e é frequentemente escrito como "1:1". Assim, a chance a:b para um certo evento é equivalente à probabilidade a/(a+b).Por exemplo, a chance 1:1 é equivalente à probabilidade 1/2 e 3:2 é equivalente à probabilidade 3/5.Ainda fica a questão de a quê exatamente pode ser atribuído uma probabilidade, e como os números atribuídos podem ser usados; isto é uma questão de interpretações de probabilidade.Há alguns que alegam que pode-se atribuir uma probabilidade a qualquer tipo de proposição lógica incerta; esta é a interpretação bayesiana. Há outros que argumentam que a probabilidade só é aplicada apropriadamente a proposições que relacionam-se com sequências de experimentos repetidos, ou da amostragem de uma população grande; esta é a interpretação frequentista. Há ainda diversas outras interpretações que são variações de um ou de outro tipo.Probabilidade na matemática
Os axiomas da probabilidade formam a base para a teoria da probabilidade matemática. O cálculo de probabilidades pode ser frequentemente determinado pelo uso da análise combinatória ou pela aplicação direta dos axiomas. As aplicações da probabilidade vão muito além da estatística, que é geralmente baseada na ideia de distribuições de probabilidade e do teorema do limite central.Para dar um significado matemático à probabilidade, considere um jogo de cara ou coroa. Intuitivamente, a probabilidade de dar cara, qualquer que seja a moeda, é "obviamente 50%"; porém, esta afirmação por si só deixa a desejar quanto ao rigor matemático - certamente, enquanto se pode esperar que, ao jogar essa moeda 10 vezes, teremos 5 caras e 5 coroas, não há garantias de que isso ocorrerá; é possível, por exemplo, conseguir 10 caras sucessivas. O que então o número "50%" significaria nesse contexto?Uma proposta é usar a lei dos grandes números. Neste caso, assumimos que é exequível fazer qualquer número de arremessos da moeda, com cada resultado sendo independente - isto é, o resultado de cada jogada não é afetado pelas jogadas anteriores. Se executarmos N jogadas, e seja NH o número de vezes que a moeda deu cara, então pode-se considerar, para qualquer N, a razão NH/N.Quando N se tornar cada vez maior, pode-se esperar que, em nosso exemplo, a razão NH/N chegará cada vez mais perto de 1/2. Isto nos permite "definir" a probabilidade Pr(H) das caras como o limite matemático, com N tendendo ao infinito, desta sequência de quocientes:Na prática, obviamente, não se pode arremessar uma moeda uma infinidade de vezes; por isso, em geral, esta fórmula se aplica melhor a situações nas quais já se tem fixada uma probabilidade a priori para um resultado particular (no nosso caso, nossa convenção é a de que a moeda é uma moeda "honesta"). A lei dos grandes números diz que, dado Pr(H) e qualquer número arbitrariamente pequeno ε, existe um número n tal que para todo N > n,Em outras palavras, ao dizer que "a probabilidade de caras é 1/2", queremos dizer que, se jogarmos nossa moeda tantas vezes o bastante, eventualmente o número de caras em relação ao número total de jogadas tornar-se-á arbitrariamente próximo de 1/2; e permanecerá ao menos tão próximo de 1/2 enquanto se continuar a arremessar a moeda.Observe que uma definição apropriada requer a teoria da medida, que provê meios de cancelar aqueles casos nos quais o limite superior não dá o resultado "certo", ou é indefinido pelo fato de terem uma medida zero.O aspecto a priori desta proposta à probabilidade é algumas vezes problemática quando aplicado a situações do mundo real. Por exemplo, na peça Rosencrantz e Guildenstern estão mortos, de Tom Stoppard, uma personagem arremessa uma moeda que sempre dá caras, uma centena de vezes. Ele não pode decidir se isto é apenas um evento aleatório - além do mais, é possível, porém improvável, que uma moeda honesta pudesse dar tal resultado - ou se a hipótese de que a moeda é honesta seja falsa.Aleatoriedade
Origem: Wikipédia, a enciclopédia livre.
A palavra aleatoriedade é utilizada para exprimir quebra de ordem, propósito, causa, ou imprevisibilidade em uma terminologia não científica. Um processo aleatório é o processo repetitivo cujo resultado não descreve um padrão determinístico, mas segue uma distribuição de probabilidade.1O termo aleatório é freqüentemente utilizado em estatística para designar uma propriedade estatística bem definida tal como um a quebra de uma neutralidade ou correlação.Equiprobabilidade
Origem: Wikipédia, a enciclopédia livre.Equiprobabilidade é uma situação, na teoria da probabilidade, em que todops os resultados possíveis são igualmente prováveis1 .Por exemplo, a cada lançamento de uma moeda a probabilidade de se obter cara é igual à probabilidade de se obter coroa. Assim, o universo das consequências possíveis, representado pelo conjunto {cara, coroa} é equiprovável.Num universo equiprovável contendo n elementos, a probabilidade de um evento unitário é: P = 1/n2 . Foi tomando por base um universo de eventos equiprováveis que Pierre-Simon Laplace lançou as bases do cálculo de probabilidades, no seu Essai Philosophique sur les Probabilités, de 1814. A sua "teoria dos acasos" procura reduzir "todos os eventos do mesmo tipo a um certo número de casos igualmente possíveis"3 .-
- --------------------------------------------------------------------------------------------------------------Matemática
- Probabilidade e raciocínio combinatório: princípios aditivo e multiplicativo. Análise de modelos clássicos para o cálculo de probabilidades: dados, moedas, formação de grupos e formação de sequências.
- Prof Walter Spinelli
- Probabilidade é a razão de dois números, onde um deles é aquilo que queremos que aconteça e o outro é o que pode acontecer em um evento aleatório.Número do evento e número do espaço amostral.
- A probabilidade tem um raciocínio combinatório.Se a sequência é determinada, a ordem da probabilidade, em eventos independentes, posso multiplicá-los.Quando se tem eventos independentes, mas pode haver trocas,se tratando em um conjunto, coloca-se um fator.
Probabilidades de loterias são probabilidades teóricos.Se comprar muitos cartões, não quer dizer que acertar com facilidade.- -----------------------------------------------------------------------------------
- Matemática
- VIDEO 11 : A Matemática do Índice de Desenvolvimento Humano (IDH) (I)
- Indicadores numéricos da qualidade de vida nos diversos países: do PIB per capita ao nascimento do IDH em 1990. A insuficiência do fator econômico (P) e a inclusão de fatores relativos à Saúde (S) e à Educação (E). As limitações da ideia de proporcionalidade e a incorporação de funções que crescem a taxas decrescentes, como a função logarítmica, nos cálculos. A presença das médias aritmética e ponderada.
- Prof Nilson Jose Machado
- A questão central é a medida da qualidade de vida nos diversos países.Até 1989, o cálculo desta medida era utilizado no cálculo do PIB.
- INDICE DE DESENVOLVIMENTO HUMANO
- - Criado em 1990 pelo economista paquistanês Mahbub Ul Haq (193401998), com a coloração de Amartya Sen, economista indiano, ganhador do prêmio nobel de economia (1998).
- - Antes, o Produto Interno Bruto (PIB) per capita era o grande indicador de desenvolvimento.
- - Com o IDH, passam a ser considerados outros indicadores, além do PIB per capita (P), indicadores como a esperança de vida (S) ao nasce, e o indice de grau de instrução (E).
- Primeiros Cálculos
- IDH = P+E+S .Esse cálculo foi utilizado durante +- 10 anos.
- 3
-
-
-
- Dólar PPC = Paridade no poder de compra.
- (igualar o valor do dólar no mundo)
Índice de Desenvolvimento Humano
Origem: Wikipédia, a enciclopédia livre.Índice de Desenvolvimento Humano (IDH) é uma medida comparativa usada para classificar os países pelo seu grau de "desenvolvimento humano" e para ajudar a classificar os países como desenvolvidos (desenvolvimento humano muito alto), em desenvolvimento (desenvolvimento humano médio e alto) e subdesenvolvidos (desenvolvimento humano baixo). A estatística é composta a partir de dados de expectativa de vida ao nascer, educação e PIB (PPC) per capita (como um indicador dopadrão de vida) recolhidos a nível nacional. Cada ano, os países membros da ONU são classificados de acordo com essas medidas. O IDH também é usado por organizações locais ou empresas para medir o desenvolvimento de entidades subnacionais como estados, cidades, aldeias, etc.O índice foi desenvolvido em 1990 pelos economistas Amartya Sen e Mahbub ul Haq, e vem sendo usado desde 1993 pelo Programa das Nações Unidas para o Desenvolvimento (PNUD) no seu relatório anual.- Haq tinha certeza de que uma medida simples, composta pelo desenvolvimento humano, seria necessária para convencer a opinião pública, os acadêmicos e as autoridades políticas de que podem e devem avaliar o desenvolvimento não só pelos avanços econômicos, mas também pelas melhorias no bem-estar humano. Sen, inicialmente se opôs a esta ideia, mas ele passou a ajudar a desenvolver, junto com Haq, o Índice de Desenvolvimento Humano (IDH). Sen estava preocupado de que seria difícil capturar toda a complexidade das capacidades humanas em um único índice, mas Haq o convenceu de que apenas um número único chamaria a atenção das autoridades para a concentração econômica do bem-estar humano.
Critérios de avaliação
A partir do relatório de 2010, o IDH combina três dimensões:- Uma vida longa e saudável: Expectativa de vida ao nascer
- O acesso ao conhecimento: Anos Médios de Estudo e Anos Esperados de Escolaridade
- Um padrão de vida decente: PIB (PPC) per capita
Até 2009, o IDH usava os três índices seguintes como critério de avaliação:- Índice de educação: Para avaliar a dimensão da educação o cálculo do IDH considera dois indicadores. O primeiro, com peso dois, é a taxa de alfabetização de pessoas com quinze anos ou mais de idade — na maioria dos países, uma criança já concluiu o primeiro ciclo de estudos (no Brasil, o Ensino Fundamental) antes dessa idade. Por isso a medição do analfabetismo se dá, tradicionalmente a partir dos 15 anos. O segundo indicador é a taxa de escolarização: somatório das pessoas, independentemente da idade, matriculadas em algum curso, seja ele fundamental, médio ou superior, dividido pelo total de pessoas entre 7 e 22 anos da localidade. Também entram na contagem os alunossupletivo, de classes de aceleração e de pós-graduação universitária, nesta área também está incluído o sistema de equivalências Rvcc ou Crvcc, apenas classes especiais dealfabetização são descartadas para efeito do cálculo.
- Longevidade: O item longevidade é avaliado considerando a expectativa de vida ao nascer. Esse indicador mostra a quantidade de anos que uma pessoa nascida em uma localidade, em um ano de referência, deve viver. Reflete as condições de saúde e de salubridade no local, já que o cálculo da expectativa de vida é fortemente influenciado pelo número de mortes precoces.
- Renda: A renda é calculada tendo como base o PIB per capita (por pessoa) do país. Como existem diferenças entre o custo de vida de um país para o outro, a renda medida pelo IDH é em dólar PPC (Paridade do Poder de Compra), que elimina essas diferenças.
- De 2008 para cá, o cálculo dos logaritmos foi aperfeiçoados.Já ocorreram duas ou três mudanças expressivas, recorrendo mais á matemática pra se ter uma representação mais fiel da realidade.
IDH: Índice de Desenvolvimento Humano
- ------------------------------------------------------------------------------------------
- Matemática
- VIDEO 12 : A Matemática do Índice de Desenvolvimento Humano (IDH) (II)
- Comparação entre as médias aritmética e geométrica: o recurso à média geométrica para a explicitação da desigualdade entre os fatores P, S e E. As desigualdades no interior de cada fator (P, S, E) e a construção do IDHAD (Índice de Desenvolvimento Humano Ajustado à Desigualdade): novo recurso à média geométrica. Outros indicadores da qualidade de vida: IDG (Índice da Diferença de Gênero).
- Prof Nilson Jose Machado
- O que preocupa o mundo nestes índices é a desigualdade social.Em uma visão macro, o mundo vai mundo bem , em todos os sentidos.
- A média geométrica tem sido o principal recurso utilizado para o índice do IDH.A media aritmética é mais democrática no sentido de combater a desilguadade.Utilizando a média aritmética e geométrica de dois números iguais, teremos o mesmo indicador.Mas quando estes números são diferentes, ao extremos, haverá uma desigualdade de resultados.A media geométrica baixa a média quando se tem indicadores de grande diferença.
- Existe dezenas de indicadores, porem o IDH é o mais conhecido.O IDH, nestes 24 anos em registrando, aprimorando estes registros e abrindo as portas ao combate á desigualdades.
- ---------------------------------------------------------------------------------------------
- Matemática
- VIDEO-AULA 13 : Representações, Gráficos, Transformações (I)
- Construção de gráficos de funções elementares e análise dos parâmetros presentes em suas equações. Análise da relação entre a expressão da função e os pontos significativos em seus gráficos.
- Prof Walter Spinelli
- Funções Elementares (f: a → b)
- Para cada e todo elemento do conjunto A, há em correspondência, apenas um elemento no conjunto B.
- A é o domínio da função e B é o contra´domínio da função.A (x) que nos dá o elemento de partida e o B (y), o elemento de contra-partida.
- Função é uma relação entre dois conjuntos, expressa por uma sentença matemática
Função (matemática)
Origem: Wikipédia, a enciclopédia livre.- Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por ƒ(x). Existem inúmeros tipos de funções matemáticas, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, função linear, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras. Cada função é definida por leis generalizadas e propriedades específicas.
Definição formal
Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:diz-se que a função f de X em Y que relaciona cada elemento x em X, um único elemento y = f (x) em Y.3Outra maneira de dizer isto é afirmar que f é uma relação binária entre os dois conjuntos tal que:- f é unívoca: se y = f (x) e z = f (x), então y = z;
- f é total: para todos x em X, existe um y em Y tal que y = f (x).
Se a segunda condição é atendida, mas a primeira não, temos uma função multivalorada, o termo função multívoca é, por vezes utilizado na mesma acepção.Se a primeira condição é atendida, mas a segunda não, temos uma função parcial.Considere as três funções seguintes:Esta não é uma função, pois o elemento 3 em X é associado com dois elementos (d e c) em Y (a correspondência é funcional). Apesar de não ser uma função, representa uma função multivalorada. Esta não é uma função, pois o elemento 1 em X não é associado com um elemento em Y. Apesar de não ser uma função, representa umafunção parcial. Esta é uma função (no caso, uma função discreta). Ela pode ser definida explicitamente pela expressão:
.- Gráficos e Transformações
- 1) Reflexões
- a) Em relação ao eixo das abscissas (horizontal) F(x) → -F(x) .O valor que é negativo, passa a ser positivo.
- b) Em relação ao eixo das ordenadas (vertical) F(x) → - F(-x). O valor que é positivo passa a ser negativo.
Reflexão (matemática)
Origem: Wikipédia, a enciclopédia livre.Em Matemática, reflexão é uma transformação geométrica que envolve um ponto a ser refletido e uma recta, transformando o ponto num outro simétrico com relação ao eixo fornecido.“Seja R uma reta no plano π. A reflexão em torno do eixo R é a transformação ρ : π → π, que associa a cada ponto X do plano o ponto X’ tal que R é a mediatriz do segmento XX’.”Construção geométrica
Podemos construir o ponto simétrico utilizando-se de régua e compasso:- Com a ponta seca em qualquer ponto da reta e raio igual à distância entre o ponto escolhido e A, trace uma circunferência;
- repita o procedimento com outro ponto da reta;
- as duas circunferências irão se encontrar em dois pontos. Um deles é A, o outro é o seu simétrico. Na reflexão, um ponto e a sua imagem estão á mesma distancia do eixo de reflexão.
- 2) Translações
- a) Em relação ao eixo das ordenadas F(x) → F(x)+k Descola verticalmente
- b) Em relação ao eixo das abscissas F(x) → F(x+k) Desloca horizontalmente
-
- Textos
gráfico de função elementar - exercícios resolvidos
- Publicado em 01/12/2013
Este vídeo integra um conjunto de conteúdos em linguagem multimídia desenvolvido para a ação piloto do Projeto Newton. Neste, o professor Marcos Monteiro Diniz apresenta a resolução de um exercício da disciplina de Cálculo 1 sobre gráfico de função elementar. - SLIDES DA VIDEO-AULA 13
- Exercícios da Video-Aula 13
-
- ---------------------------------------------------------------------------------------
- Matemática
- VIDEO-AULA 14 : Representações, Gráficos, Transformações (II)
- Análise das transformações isométricas (translação e reflexão) causadas nos gráficos de funções elementares (polinomiais de 1º e de 2º graus, exponencial e logarítmica) pela introdução de determinados parâmetros em suas equações. A simetria apresentada nos gráficos cartesianos de uma função e de sua inversa em relação à reta bissetriz dos quadrantes ímpares.
- Prof Walter Spinelli
- Função Polinomial de 1º Grau F(x)=ax+b
-
- Função Polinomial de 2º Grau F(x)=ax2
-
-
- Função Polinomial de 2º Grau F(x+p)+q=a(x+p)2+q
-
- Função Polinomial de 2º Grau y=ax2+bx+c para y=a(x+p)2+q
-
- ---------------------------------------------------------------------------------------
- Matemática
O modelo da esfera para estudar a Terra. Eratóstenes e a medida da circunferência da Terra. Kepler e o movimento elíptico de translação dos planetas em torno do Sol. Definição da elipse como lugar geométrico. As três leis de Kepler.
Prof Jose Luiz Pastore Neto
Dentre as inúmeras formas geométricas tridimensionais, a esfera é uma das mais importantes, devido ás suas aplicações, mecanismos (rolamentos, GPS).
Já nas figuras planas ,a circunferências e a elipse, são, também, duas figuras importantes.Esta aula vai utilizar como referência a Terra, sua geometria, seus movimentos e forma para investigar as três figuras geométrica.
Eratóstenes (250 a.C), matemático, geógrafo, cientísta grego trabalhou com esta idéia da esfericidade da Terra, as medidas da Terra.Foi diretor da Biblioteca Central de Alexandria, cuidava de mais de 700 mil rolos de papiro de conhecimentos da época.
Ele ficou sabendo que em uma na cidade de Ciene, em um determinado dia do ano, o Sol ficava em uma posição que não produzia sombra, á 850 km de Alexandria.A partir daí, deu-se os cálculos das medidas da Terra.
A forma da Terra não é totalmente redonda, ela é levemente achatada os polos, forma conhecida como elipsóide.A Terra é uma esfera, para efeitos de estudos.
Baseado na teoria de Ptolomeu até o séc XV, a Terra era o centro e os planetas, corpos celestes giravam em torno de si, modelo geocentrísta.Depois do séc XVI, Copérnico propôs um modelo heliocentrico, o Sol sendo o centro e os planetas á sua volta, com órbita circular;Galileu defendeu esta idéia, coletando dados do Céu com sua invenção, a luneta, em 1609, confirmando a idéia heliocentrísta.
Kepler, contemporâneo de Galileu, propôs 3 leis sobre sua teoria de os planetas terem movimentos circulares:
1ª Lei: os planetas tinhas movimentos elipticos em torno do Sol, levemente circular.
Teorema de Pitágoras: a2 = b2 + c2
Plano Cartesiano: x2 + y2 = 1
a2 b2
Excentricidade da Elipse: e = c
a
2ª Lei: defende que a Terra gira mais rápido próximo do Sol do que quando está mais distante.
3ª Lei: o quadrado do período é diretamente proporcional ao cubo do raio médio.
T2 = kr3
Esta proporcionalidade entre o período, o raio médio e o semi-eixo maior nos permite calcular a duração de um ano em determinado planeta
------------------------------------------------------------------------------------
- Matemática
VIDEO-AULA 16 : Geometria da esfera: da Terra ao GPS (II)
A localização sobre a Terra: coordenadas geográficas e coordenadas cartesianas. Equação analítica da esfera e do plano. O modelo geométrico de funcionamento do GPS: teorema das quatro esferas. Interpretação analítica e geométrica de um sistema de equações.
Prof Jose Luiz Pastore Neto
Podemos medir a distância entre dois pontos por meio de uma reta ? Se tratando de esfera, não ! Só se o mapa for apropriado.
COMO LOCALIZAR UM PONTO PELO GPS
É possivel sabermos a distância entre um satélite e a Terra ?
Teorema das quatro esferas: uma esfera tem seu raio; duas esferas intersectam formando um raio menor; tres esferas intersectadas formam um raio ainda menor com dois pontos; quando a quarta esfera intersecta, fecha em um ponto.
São 24 satélites orbitando ao redor da Terra.Quando ponto da Terra recebe informação de pelo menos 4 satélites, estas informações produzem intersecção de 4 esferas não coplanares (3 satélites + Terra) gerando um intersecção onde será o ponto localizado na Terra.
O estudo da esfera mostrou-se importante na compreensão na matemática do GPS e em estudo de engenharia, na compreensão de mecanismos, rolamentos, sendo fundamental.
Texto - Geometria do Globo Terrestre
Texto - Earth Observatory
Texto - Elementos geométricos
------------------------------------------------------------------------------------------
Matemática
VIDEO-AULA 17 : Otimização, Programação Linear (I)
A ideia de otimização: mais do que resolver um problema, otimizar é encontrar a melhor maneira possível de resolvê-lo, o que conduz a situações em que se busca um máximo ou um mínimo de alguma grandeza. Fenômenos lineares : exemplos de formulação de problemas de otimização. Proporcionalidade, função do primeiro grau, equação da reta. Representação de regiões do plano por igualdades ou desigualdades. Equacionamento de problemas lineares simples de máximos e mínimos.
A ideia de otimização: mais do que resolver um problema, otimizar é encontrar a melhor maneira possível de resolvê-lo, o que conduz a situações em que se busca um máximo ou um mínimo de alguma grandeza. Fenômenos lineares : exemplos de formulação de problemas de otimização. Proporcionalidade, função do primeiro grau, equação da reta. Representação de regiões do plano por igualdades ou desigualdades. Equacionamento de problemas lineares simples de máximos e mínimos.
------------------------------------------------------------------------------------------
Matemática
Video-Aula 18 :Otimização, Programação Linear (II)Exploração de propriedades das retas e dos coeficientes de suas equações para a caracterização da região de viabilidade para um problema: interseção com eixos, interseção entre retas, paralelismo. Resolução de Problemas lineares simples de otimização (máximos ou mínimos). Análise dos resultados. Variáveis que foram deixadas de lado na modelagem e no equacionamento dos problemas. Prof Nilson Jose Machado


----------------------------------------------------------------------
Matemática
Video 19 : Expoentes e logaritmos em diferentes contextos (I)A ideia da representação de números muito grandes ou muito pequenos como potências de 10: se N = 10x, então x é o logaritmo de N. O significado prático dos logaritmos na simplificação de cálculos, no século XVII: tábuas. A importância atual dos logaritmos em diferentes contextos: a escala Richter para a avaliação de terremotos; o pH (potencial Hidrogeniônico) para a indicação da acidez de um líquido; a escala em deciBéis para a medida da intensidade sonora. Prof Nilson Jose Machado
LOGARÍTMOS E EXPOENTES
LOGARÍTMOS E EXPOENTES
Este assunto deu início por volta dos anos de 1700.Percebeu-se faltar controle com números muito grandes.Números até dez era de fácil percepção, mas os grandes dava trabalho.100.000 = 10 elevado á 4 fica mais fácil a visualização, por isso passou a pensar em logarítmos.
Nos dias dias atuais não se preocupam mais em simplificar cálculos.As aplicações dos logarítmos são mais significativas do que simplificar cálculos.A idéia dos logarítimos é trazer uma equação igual ao exemplo abaixo e simplificar.
Além disso, utiliza-se estas simplificações na ESCALA RICHTER, Acidez (Ph), decibeis, juros compostos.
Onde o expoente é a questão, o logarítimo é a solução.
Números muito grandes ou muito pequenos,a estratégia que se leva ao logarítmo, é reduzir estes números á um expoente.
-------------------------------------------------------------------------------------------
Matemática
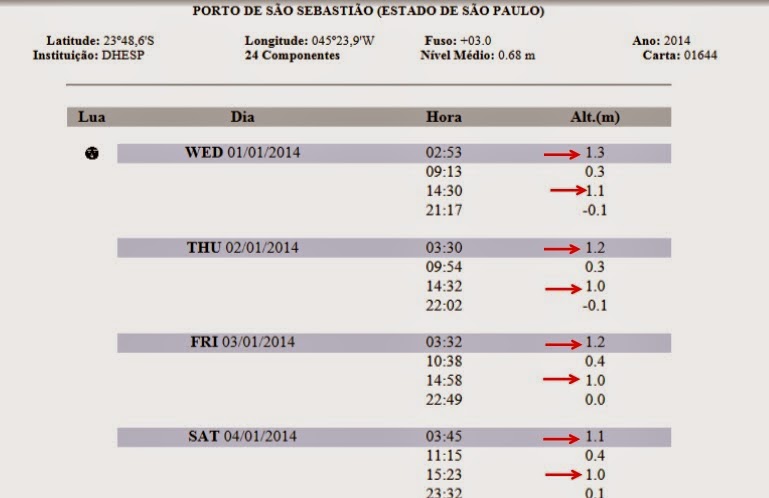
Video 20 - Expoentes e logaritmos em diferentes contextos (II)Logaritmos em outras bases, diferentes de 10. Propriedades dos expoentes e das potências estendidas aos logaritmos. Como calcular logaritmos em diferentes bases, a partir dos valores conhecidos em uma dada base. O número e = 2,71828..., significado no cálculo de juros e no crescimento de populações. A função logarítmica como inversa da exponencial. Prof Nilson Jose Machado




-----------------------------------------------------------------------------------------
Matemática
Video-Aula 22 -Proporcionalidade e periodicidade na natureza (II)Análise do modelo físico constituído por um sistema do tipo massa-mola e o significado das equações do Movimento Harmônico Simples (MHS). Análise das características de gráficos de funções do tipo y = A + Bsen(Cx + D) e interpretação dos significados gráficos dos parâmetros presentes na equação.dade
Na circunferência temos um gráfico de uma função trigonométrica, seno e coseno.Um posição mostra a velocidade e o outra , o ponto .
Uma sentença matemática de uma função com vários parâmetros.Constantes que interferem no formato da curva.
Na circunferência temos um gráfico de uma função trigonométrica, seno e coseno.Um posição mostra a velocidade e o outra , o ponto .

Uma sentença matemática de uma função com vários parâmetros.Constantes que interferem no formato da curva.
------------------------------------------------------------------------
Matemática
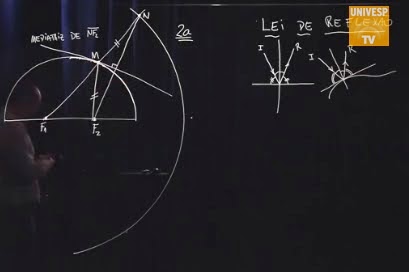
Video-aula 23 -Cônicas aplicadas em problemas de engenharia (I)
Definição das cônicas por meio de secções em um cone. Definição das cônicas como lugar geométrico. Visualização das cônicas por meio de aplicativo de geometria dinâmica (Geogebra). Excentricidade de uma cônica. Propriedade focal da parábola. Parábolas, paraboloides e o farol dos automóveis.
A elipse, a hipérbole e a parábola são três curvas de suma importância no estudo da ciência exatas aplicadas.Este conjunto de 3 curvas leva o nome de CÔNICAS,devido elas aparecerem por meio da intersecção, do cruzamento de um plano em relação á superfície de um cone.


Esta imagem permite observar todas as curvas ao mesmo tempo.



Slides da Video-aula 23
Exercícios da Video-aula 23

------------------------------------------------------------------------------------
A elipse, a hipérbole e a parábola são três curvas de suma importância no estudo da ciência exatas aplicadas.Este conjunto de 3 curvas leva o nome de CÔNICAS,devido elas aparecerem por meio da intersecção, do cruzamento de um plano em relação á superfície de um cone.


Esta imagem permite observar todas as curvas ao mesmo tempo.



Slides da Video-aula 23
Exercícios da Video-aula 23

------------------------------------------------------------------------------------
Matemática
--------------------------------------------------------------------------------------------
Matemática
A combinação destas perspectivas vai nos levar ás idéias e funções matemáticas, necessárias á descrição deste fenômeno.Uma função do 1º grau, exponencial ou um logarítmo.
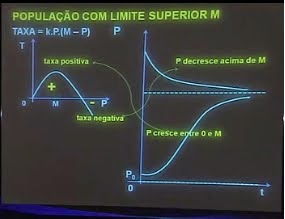
Video-aula 26 -Modelos de crescimento de populações: taxas de variação (II)O número e= 2,71828...: significado em diferentes contextos envolvendo crescimento ou decrescimento (juros, populações, decaimento radioativo). Modelos de crescimento de população com o estabelecimento de um valor máximo a ser atingido: análise qualitativa e curva logística. Modelos de crescimento com um teto e com um limite inferior para a população (problema da extinção de espécies): análise qualitativa e soluções de equilíbrio.Prof Nilson José Machado (E) = 2,71828...(pi) = 3,141592...


----------------------------------------------------------------------------------------- MatemáticaVideo-aula 27 -Números complexos e transformações no plano (I)Discussão a respeito da evolução dos conjuntos numéricos e da introdução histórica dos números complexos como o mais amplo dos conjuntos. A álgebra dos números complexos e sua importância relativa no estudo das funções, principalmente as polinomiais. O plano de Argand-Gauss e os operadores complexos. Prof Walter SpineliAbaixo um problema de geometria muito simples: uma equação do 3º grau
------------------------------------------------------------------------------- MatemáticaVideo-aula 28 - Números complexos e transformações no plano (II)Construção do significado dos números complexos enquanto operadores de transformações no plano; significado das operações. Transformações no plano: números complexos e os fractais.
Matemática
Video 25 : Modelos de crescimento de populações: taxas de variação (I)Evolução da população do mundo nos dois últimos milênios: taxas de crescimento e projeções. A variação na unidade de tempo e os três tipos de crescimento: taxas constantes, taxas crescentes, taxas decrescentes. Projeções aritméticas e geométricas: o erro de Malthus no final do século XVIII. A articulação entre os três tipos de crescimento: primeira ideia da curva logística; análise qualitativa de modelos de crescimento a taxas constantes; e taxas proporcionais ao valor da população em cada instante.Prof Nilson José Machado
A combinação destas perspectivas vai nos levar ás idéias e funções matemáticas, necessárias á descrição deste fenômeno.Uma função do 1º grau, exponencial ou um logarítmo.
Modelos de Crescimento de Populações
- Taxa Constante
- Taxa Crescente
A taxa de crescimento é proporcional ao valor da população.
Malthus , em 1798, ficou famoso com algumas previsões: previu que em um determinado ano não teria alimento para a população devido ao seu rápido crescimento.Não se cumpriu devido a diminuição do consumo de alimentação e a população também.O produção de alimentos, hoje, cresce mais do que a população devido ás máquinas.
Curva Logística
Esses fenômenos de crescimento de população são melhores descritos através da Curva Logistica, uma curva em "S", modelos mais próximo do que acontece.
-----------------------------------------------------------------------------------------
Matemática
Video-aula 26 -Modelos de crescimento de populações: taxas de variação (II)O número e= 2,71828...: significado em diferentes contextos envolvendo crescimento ou decrescimento (juros, populações, decaimento radioativo). Modelos de crescimento de população com o estabelecimento de um valor máximo a ser atingido: análise qualitativa e curva logística. Modelos de crescimento com um teto e com um limite inferior para a população (problema da extinção de espécies): análise qualitativa e soluções de equilíbrio.Prof Nilson José Machado (E) = 2,71828...(pi) = 3,141592...


----------------------------------------------------------------------------------------- MatemáticaVideo-aula 27 -Números complexos e transformações no plano (I)Discussão a respeito da evolução dos conjuntos numéricos e da introdução histórica dos números complexos como o mais amplo dos conjuntos. A álgebra dos números complexos e sua importância relativa no estudo das funções, principalmente as polinomiais. O plano de Argand-Gauss e os operadores complexos. Prof Walter SpineliAbaixo um problema de geometria muito simples: uma equação do 3º grau
------------------------------------------------------------------------------- MatemáticaVideo-aula 28 - Números complexos e transformações no plano (II)Construção do significado dos números complexos enquanto operadores de transformações no plano; significado das operações. Transformações no plano: números complexos e os fractais.
VIDEO - DIMENSION
----------------------------------------------------------------------------












































































































































Nenhum comentário:
Postar um comentário